Tutorial: Triangular Arbitrage on Bitstamp

Triangular Arbitrage is one of the most natural methods of Arbitrage primarily because is not between exchanges, but rather it is between pairs (BTC/USD, BTC/ETH … etc.) on a single exchange. Traditional Arbitrage requires transferring assets between the exchanges which is slow and painful. The longer the trades take to complete the Arbitrage, the more risk you incur (though there are methods to work around transferring assets between exchanges). In Triangular Arbitrage, you increase the amount of the initial asset you own by trading through a chain of other assets, eventually trading back to the initial asset.

This example is drawn from investopedia: Suppose you have $1 million and you are provided with the following exchange rates: EUR/USD = 0.8631, EUR/GBP = 1.4600 and USD/GBP = 1.6939.

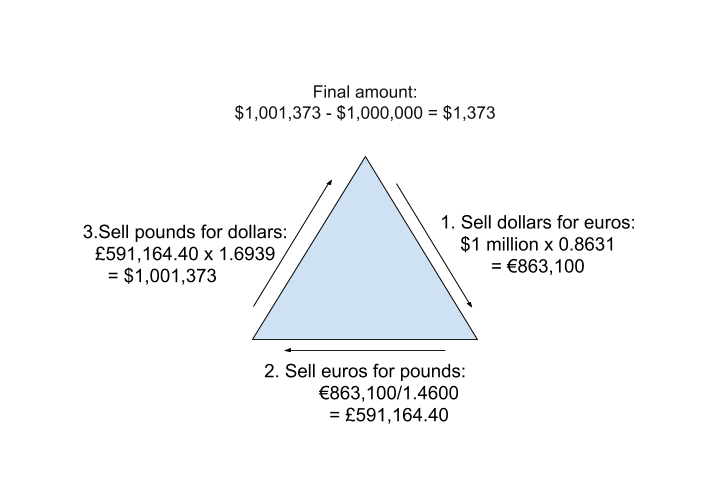
With these exchange rates there is an arbitrage opportunity:

Sell dollars for euros: $1 million x 0.8631 = €863,100 Sell euros for pounds: €863,100/1.4600 = £591,164.40 Sell pounds for dollars: £591,164.40 x 1.6939 = $1,001,373 Subtract the initial investment from the final amount: $1,001,373 - $1,000,000 = $1,373 From these transactions, you would receive an arbitrage profit of $1,373 (assuming no transaction costs or taxes).

We will now write code that finds Triangular Arbitrage opportunities on Bitstamp.

The Bitstamp client we will be using was writen by Kamil Madac, and can be found on github

We will start by importing a few python libraries:

import bitstamp.client
import threading
import numpy as np
from collections import defaultdict

Kamil Madac’s client makes it easy to start a session with Bitstamp:

public_client = bitstamp.client.Public()

We can then use this client to pull data from Bitstamp. The first thing we need to know is all the pairs that exist on the exchange:

 pairs = public_client.trading_pairs_info()

which returns a list of dictionaries:

 [ {'base_decimals': 8, 'minimum_order': '5.0 USD', 'name': 'LTC/USD', 'counter_decimals': 2,
  'trading': 'Enabled', 'url_symbol': 'ltcusd', 'description': 'Litecoin / U.S. dollar'}, ...]

We will use the pair information to pull down the ticker value for each pair. Because we want to get the ticker value for every pair at as close to the same time as possible we will make a multithread call to the Bitstamp:

tickers = []

def get_ticker(base, quote):
    ticker = public_client.ticker(base=base, quote=quote)
    ticker['base'] = base
    ticker['quote'] = quote
    ticker['ask'] = float(ticker['ask'])
    ticker['bid'] = float(ticker['bid'])
    tickers.append(ticker)
    
threads = []
for pair in pairs:
    base, quote = pair['name'].split('/')
    thread = threading.Thread(target=get_ticker, args=(base, quote,))
    thread.start()
    threads.append(thread)

for thread in threads:
    thread.join()

Next, we will define the exchange fee as a flat 0.25% per trade:

exchange_fee = 0.0025

Now to compute the cost of trading through different pairs, we will build up a couple of useful data structures: a set with each unique symbol/ticker, a dictionary with the conversion rates, and an index for each symbol/ticker.

unique_symbols = set(x['base'] for x in tickers) | set(x['quote'] for x in tickers)
conversion_rates = defaultdict(dict)
for ticker in tickers:
    conversion_rates[ticker['quote']][ticker['base']] = {'bid':ticker['bid'], 'ask':ticker['ask']}
    conversion_rates[ticker['base']][ticker['quote']] = {'bid':1.0/ticker['ask'], 'ask':1.0/ticker['bid']}

#BTC is going to be the start node
graph_symbol_lookup = {'BTC':0}
for ticker in tickers:
    if ticker['base'] not in graph_symbol_lookup:
        graph_symbol_lookup[ticker['base']] = len(graph_symbol_lookup)
    if ticker['quote'] not in graph_symbol_lookup:
        graph_symbol_lookup[ticker['quote']] = len(graph_symbol_lookup)
graph_symbol_reverse_lookup = {y:x for x, y in graph_symbol_lookup.items()}

Now comes the fun part. For simplicity, we are using three loops O(n^3) which is very….very bad. This could be better done by modifying something like Dijkstra, but it would make it harder to understand so we will do it the wrong way.

Loops through every combination of currency pairs and computes the profit or loss by trading through them if the profit loss is positive then you found an opportunity for Triangular Arbitrage.

for i in range(0, len(unique_symbols)):
  for j in range(0, len(unique_symbols)):
      for k in range(0, len(unique_symbols)):
      
          #Make sure we have selected 3 unique coins by index
          if len(set([i, j, k])) != 3:
              continue
          
          #Load the coins from the graph
          c1 = graph_symbol_reverse_lookup[i]
          c2 = graph_symbol_reverse_lookup[j]
          c3 = graph_symbol_reverse_lookup[k]
          
          #We start with 1.0 coins of c1
          initial_equity = current_equity = 1
          
          #Some conversions dont exist, skip these
          if c2 not in conversion_rates[c1] or c3 not in conversion_rates[c2] or c1 not in conversion_rates[c3]:
              #No conversion is avalible 
              #print('No conversion for {} -> {} -> {} -> {}'.format(c1, c2, c3, c1))
              continue 
          
          #Trade through the selected coins c1->c2->c3->c1, purchasing at the 'ask' price and paying the fee for each trade
          current_equity -= current_equity*exchange_fee
          current_equity = current_equity * conversion_rates[c1][c2]['ask'] 
          current_equity -= current_equity*exchange_fee
          current_equity = current_equity * conversion_rates[c2][c3]['ask']
          current_equity -= current_equity*exchange_fee
          current_equity = current_equity * conversion_rates[c3][c1]['ask']

          #Profit/loss is in terms of the starting coin
          profit_loss = current_equity - initial_equity                    
          print('{} -> {} -> {} -> {} profit/loss = {} {}'.format(c1, c2, c3, c1, c1, profit_loss))

What we have just done is the easy part. Now you need to successfully execute the three trades before any of the prices change. This will require looking at the depth of the order book so, you know how much you can trade as well as holding each currency so that you can simultaneously execute all the orders. Have fun.

nharmon8/jnkopacz